Toán và Tin — Học toán để làm gì?

toan-va-tin

Toán học & Học toán

Xin chào, mấy hôm nay dịch quá, mình rảnh rỗi ngoài việc làm hồ sơ chuẩn bị đi làm thì cũng chẳng biết làm gì, thế là ngồi luyện algorithms và học thêm vài thứ linh tinh. Nhưng trong lúc Youtube kiếm nhạc relax, vô tình lỡ nhấn vào Facebook, mình mất mẹ nó một ngày cho cái trò infinity scroll.

Trong lúc lướt face, mình thấy cái meme sau:

Dựa lưng vào ghế, mình nghiệm lại từ những ngày lọt lòng mẹ, mình được làm quen với những con số vào mẫu giáo, Cấp 1 vật vã với bảng cửu chương, bài toán chia đều, tới giờ vẫn không rõ là mình có thuộc bảng 7 và 8 hay không Cấp 2 còn nhiều thứ đau não hơn, đó là những bài tìm x, biểu thức đột biến, đa thức,… Và tới cấp 3, cũng chẳng rõ là học cái gì, tích phân vi phân, hình không gian, lượng giác,…

Lên đại học, tưởng chừng thoát được toán, nhưng đời lại vả vào mồm mình bằng những thứ bá đạo hơn trong cái tên bá đạo hơn: Toán cao cấp. Là những bài Tích phân, vi phân nhưng độ khó hiểu cao hơn, vẫn là Xác xuất thống kê nhưng có chuồng bồ câu Ma trận và những người bạn.

Chưa kể bộ môn Toán và người bạn thân của Toán: Vật Lý

Mình bắt đầu suy nghĩ xem việc học toán có giúp ích gì ngoài việc tính lại hoá đơn ở quán nhậu và đứng lên đấm vào mồm thằng chủ quán nhậu nếu bạn phát hiện nó không biết cộng trừ nhân chia.

Học toán có ích gì?

Không phải chỉ riêng ngành công nghệ, rất nhiều ngành nghề đều cần sử dụng toán, nhưng vẫn dừng lại ở mức độ cơ bản: Cộng trừ nhân chia hoặc cấp số cộng, cấp số nhân. Vậy học nhiều như thế để làm gì?

Nói về mấy năm đi code, hồi trước nhiều khi có mấy anh chị nói suốt: “Học toán đi, không học toán thì làm sao học được IT?”. Nghe xong cảm giác con đường mình đi có vẻ gian truân hơn nhiều, đam mê như thế… chẳng lẽ bỏ ngang?

Thế mà đi học, toán một kiểu, tin học một kiểu, tìm mãi vẫn chẳng thấy liên quan chỗ nào. Cấp 3 học Pascal, cuối cùng liên quan ở chỗ… Viết phần mềm nhập vào các số $a, b, c$ của đẳng thức $ax^2 + bx + c = 0$ rồi tìm $x$

Thế là chẳng còn bận tâm gì nữa, đi học IT thôi, có liên quan mẹ gì tới toán đâu?

Sau đó mình đi làm, nghiệm ra điều đó càng được khẳng định hơn khi những project đó chỉ xoay quanh CRUD¹ Cảm giác thoát khỏi toán thật tuyệt. Nghe bảo làm game cũng cần toán, thử dùng Unity mà xem, engine nó hỗ trợ hết rồi.

Kết luận: Toán cũng không quan trọng lắm

Toán ứng dụng

Câu chuyện bên trên để các bạn cũng hiểu một phần là tác giả bài viết không ưa gì Toán, và viết từ góc nhìn cá nhân nên chắc cũng sẽ gây ra tranh cãi. Tuy nhiên nói đi cũng phải nói lại, nếu bạn đi theo hướng nghiên cứu hoặc muốn học sâu vào việc implement một vấn đề, bạn không thể không học Toán, vì Toán học là bản chất của gần như mọi vấn đề.

Gần đây mình có gặp một vấn đề về algorithm trong canvas cần phải implement: Làm sao để detect 2 object chạm vào nhau, sau đó áp dụng chuyển động đàn hồi (elastic collision) để di chuyển 2 object đó sau va chạm. Thế là vò đầu bứt tai đi đọc đủ thứ tài liệu.

Vấn đề 1: Collision detection - Phát hiện va chạm

Nếu 2 object là hình vuông, thông thường chúng ta chỉ cần kiểm tra xem 1 trong 4 cạnh của object A có nằm trong object B hay không

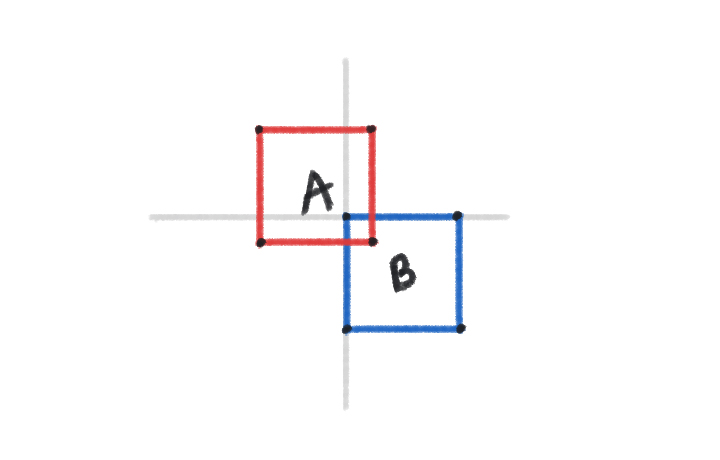
Dễ dàng chúng ta sẽ có:

 1let a = { x: 5, y: 5, width: 50, height: 50 }
 2let b = { x: 20, y: 10, width: 10, height: 10 }
 3
 4if (
 5  a.x < b.x + b.width &&
 6  a.x + a.width > b.x &&
 7  a.y < b.y + b.height &&
 8  a.y + a.height > b.y
 9) {
10  alert("Collision detected!")
11}

Nếu 2 object là hình tròn, thì khá đơn giản hơn, vì chỉ cần kiểm tra khoảng cách giữa 2 tâm hình tròn có nhỏ hơn tổng bán kính 2 hình tròn hay không là được:

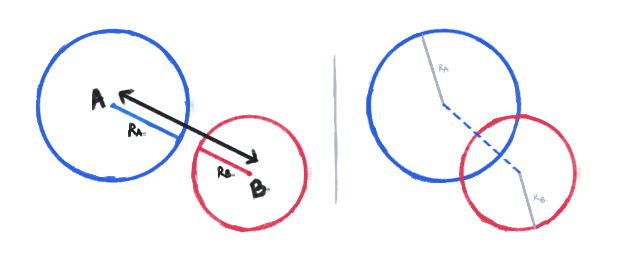
Từ công thức:

f(a, b) = \sqrt{(x_a - x_b)^2 + (y_a - y_b)^2} \lt r_a + r_b

 1let a = { x: 5, y: 5, radius: 20 }
 2let b = { x: 12, y: 10, radius: 12 }
 3
 4var dx = a.x - b.x
 5var dy = a.y - b.y
 6var distance = Math.sqrt(dx ** 2 + dy ** 2)
 7
 8if (distance < a.radius + b.radius) {
 9  alert("Collision detected!")
10}

Cơ bản là như thế, cũng khá dễ phải không?

Vấn đề 2: Elastic collision - Va chạm đàn hồi

Va chạm đàn hồi, tức là va chạm giữa hai vật thể, trong đó tổng động năng của hai vật thể không thay đổi

Kết quả

Để mà nói thì vấn đề này khá phức tạp vì nó đụng vào Toán học và Vật lý rất nhiều, sau đó từ vấn đề Toán Lý, chúng ta phải chuyển nó về Tin học, vậy nên phần này khá nặng lý thuyết, mình cũng sẽ cố diễn giải theo cách dễ hiểu nhất.

Trước hết, chúng ta cần phải hiểu va chạm đàn hồi hoạt động như thế nào: Xét các vật 1 và 2 có khối lượng $m_1$ và $m_2$ và vận tốc $u_1$ và $u_2$ trước khi va chạm, và $v_1$ và $v_2$ sau khi va chạm. Như đã nói ở định nghĩa, tổng động năng sẽ không thay đổi sau khi va chạm, nên động năng được bảo toàn.

Việc bảo toàn động lượng toàn phần trước và sau va chạm được thể hiện bằng công thức:

m_1u_1 + m_2u_2 = m_1v_1 + m_2v_2

Tương tự vậy, việc bảo toàn động năng sẽ được biểu thị bằng cách:

\frac{1}{2}m_1u_1^2 + \frac{1}{2}m_2u_2^2 = \frac{1}{2}m_1v_1^2 + \frac{1}{2}m_2v_2^2

Chúng ta có thể tìm $v_1, v_2$ khi biết $u_1, u_2$ bằng cách:

v_1=\frac{m_1-m_2}{m_1+m_2}u_1 + \frac{2m_2}{m_1+m_2}u_2

v_2=\frac{2m_1}{m_1+m_2}u_1 + \frac{m_2-m_1}{m_1+m_2}u_2

Nếu khối lượng hai vật bằng nhau, chúng ta dễ dàng triệt tiêu và rút gọn công thức chỉ còn lại:

v_1=u_2

v_2=u_1

Giờ thì dễ hiểu hơn rồi, đơn giản là tương ứng với các vật thể có khối lượng bằng nhau, thì chúng trao đổi vận tốc ban đầu với nhau.

Ví dụ:

Quả bóng	A = 3kg	B = 5kg
Trước va chạm	4 m/s	-6m/s
Sau va chạm	-8.5 m/s	1.5 m/s

Để dễ hình dung, mời bạn xem qua các mẫu va chạm sau:

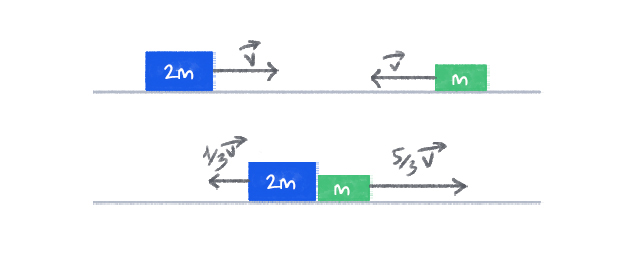
Va chạm giữa 2 vật thể không cùng khối lượng

2 vật thể không cùng khối lượng va chạm ngược chiều với cùng vận tốc, khối lượng không bằng nhau, sau khi va chạm, động năng được bảo toàn, khối lượng không thay đổi, vì vậy áp dụng công thức ta có được vận tốc của 2 vật sau va chạm:

v_1 = \frac{2m - m}{2m + m}v + \frac{2m}{2m + m}(-v) = \frac{1}{3}v - \frac{2}{3}v = -\frac{1}{3}v

v_2 = \frac{2.2m}{2m + m}(-v) + \frac{m - 2m}{2m + m}v = -\frac{4}{3}v - \frac{1}{3}v = -\frac{5}{3}v

Va chạm giữa 2 vật thể cùng khối lượng

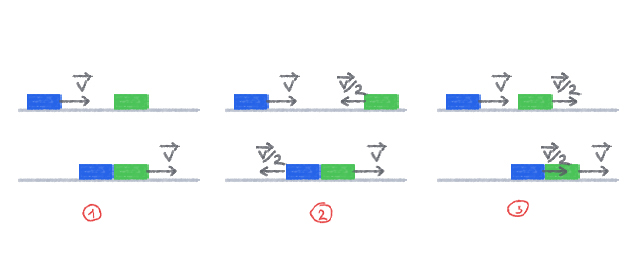
Ở trường hợp 2 vật thể có cùng khối lượng, hãy thử lấy nhiều ví dụ hơn:

Khi vật A chuyển động với vận tốc $\vec{v}$ chạm vào vật B đứng yên, vật B sẽ di chuyển với vận tốc bằng $\vec{v}$ , vật A sau va chạm sẽ đứng yên.
Khi vật A chuyển động với vận tốc $\vec{v}$ , vật B di chuyển ngược chiều với vận tốc $-\frac{1}{2}\vec{v}$ . Sau va chạm, chúng đổi chiều và hoán đổi vận tốc cho nhau.
Khi vật A và B chuyển động cùng chiều với vận tốc lần lượt là $\vec{v}$ và $\frac{1}{2}\vec{v}$ , sau một thời gian vật A chạm vào vật B, chúng vẫn di chuyển cùng chiều và hoán đổi vận tốc cho nhau.

Như vậy, chúng ta có thể tạm thời phân tích xong cách để xử lý va chạm đàn hồi, giờ thì từ toán sang tin nàoooo

Vấn đề 3: Từ Toán Lý đến Tin học

Đầu tiên, khởi tạo một hàm giải quyết việc va chạm:

 1/**
 2 * Hoán đổi vận tốc x và y của hai vật thể sau khi va chạm
 3 *
 4 * @param  Object | particle
 5 * @param  Object | otherParticle
 6 * @return null
 7 */
 8const resolveCollision = (particle, otherParticle) => {
 9  // Độ chênh lệch của vận tốc
10  const xVelocityDiff = particle.velocity.x - otherParticle.velocity.x;
11  const yVelocityDiff = particle.velocity.y - otherParticle.velocity.y;
12
13  // Độ chênh lệch về khoảng cách
14  const xDist = otherParticle.x - particle.x;
15  const yDist = otherParticle.y - particle.y;
16
17  // Lưu lại khối lượng trong biến để dễ đọc hơn
18  // Tuy nhiên việc này sẽ tạo ra thêm bộ nhớ, hãy cân nhắc khi áp dụng
19  const m1 = particle.mass;
20  const m2 = otherParticle.mass;
21
22  ...

Chúng ta phải xác định rằng các vật thể không bị chồng chéo lên nhau, vì các vật thể chồng lên nhau như thế không thể xử lý được va chạm:

1  ...
2
3  if (xVelocityDiff * xDist + yVelocityDiff * yDist >= 0) {
4    // handle goes here
5  }

Góc của 2 vật thể va chạm bằng atan2²

1const angle = -Math.atan2(
2  otherParticle.y - particle.y,
3  otherParticle.x - particle.x,
4)

Viết hàm tính vận tốc trước va chạm bằng cách xoay lại hệ toạ độ để tìm ra vận tốc ban đầu của vật thể:

 1/**
 2 * Xoay lại hệ toạ độ để tính vận tốc
 3 *
 4 * Lấy vận tốc sau đó thay đổi theo hệ toạ độ mới được xoay
 5 *
 6 * @param  Object | velocity | Vận tốc của một vật riêng lẻ
 7 * @param  Float  | angle    | Góc va chạm giữa 2 vật tính theo radian
 8 * @return Object | Trả về vận tốc x và y bị thay đổi sau khi xoay hệ toạ độ
 9 */
10
11const rotate = (velocity, angle) => {
12  x: velocity.x * Math.cos(angle) - velocity.y * Math.sin(angle),
13  y: velocity.x * Math.sin(angle) + velocity.y * Math.cos(angle)
14}

Giờ thì bắt đầu xử lý va chạm theo toán học được rồi:

 1// Vận tốc của các vật thể trước phương trình
 2const u1 = rotate(particle.velocity, angle)
 3const u2 = rotate(otherParticle.velocity, angle)
 4
 5// Vận tốc của các vật thể sau khi va chạm 1 chiều:
 6const v1 = {
 7  x: (u1.x * (m1 - m2)) / (m1 + m2) + (u2.x * 2 * m2) / (m1 + m2),
 8  y: u1.y,
 9}
10const v2 = {
11  x: (u2.x * (m1 - m2)) / (m1 + m2) + (u1.x * 2 * m2) / (m1 + m2),
12  y: u2.y,
13}
14
15// Vận tốc chính xác của vật thể sau khi quay hệ toạ độ trở lại như ban đầu
16const vf1 = rotate(v1, -angle)
17const vf2 = rotate(v2, -angle)
18
19// Hoán đổi lại vận tốc thực cho các vật thể
20
21particle.velocity.x = vf1.x
22particle.velocity.y = vf1.y
23otherParticle.velocity.x = vf2.x
24otherParticle.velocity.y = vf2.y

Hoàn thành!

Kết quả chúng ta có được

Tại sao phải xoay lại hệ toạ độ?

Gọi $a$ là góc va chạm giữa 2 vật thể, chúng ta có thể hình dung va chạm như sau:

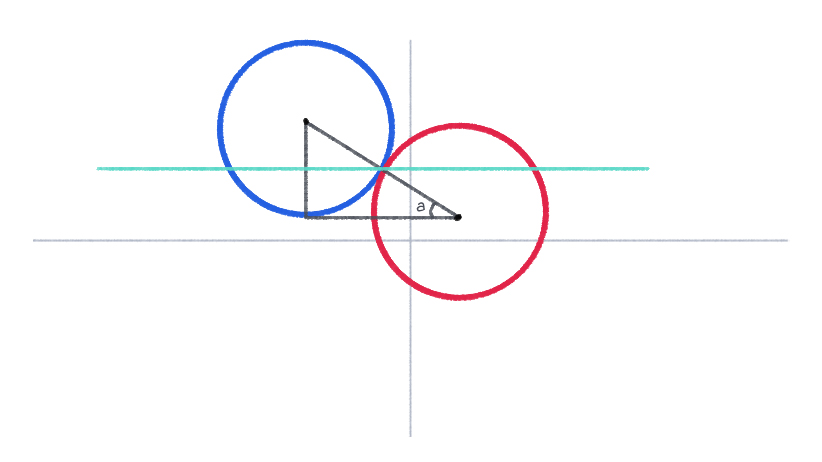
Có thể thấy, vận tốc vật không thể tính như một vector thông thường trong tin học vì tâm của 2 vật thể hình tròn không cùng nằm trên 1 đường thẳng song song với trục toạ độ x.

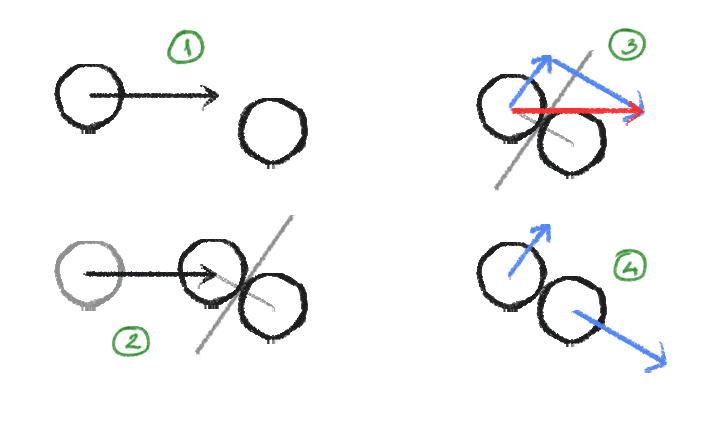
Và như đã nói, góc lượng giác ngược $a$ trả về giá trị radian từ $-\pi$ tới $\pi$ giữa trục toạ độ x và tia từ gốc toạ độ $(0, 0)$ tới điểm $(x, y)$ , thế nên ta cần phải xoay cả hệ toạ độ lại sao cho đƯờng thẳng nối tâm của 2 vật thể hình tròn nằm song song cùng trục toạ độ x.

Vì vậy khi xoay hệ toạ độ lại bằng một góc $a$ radian, chúng ta có thể tính được vận tốc vật trước va chạm

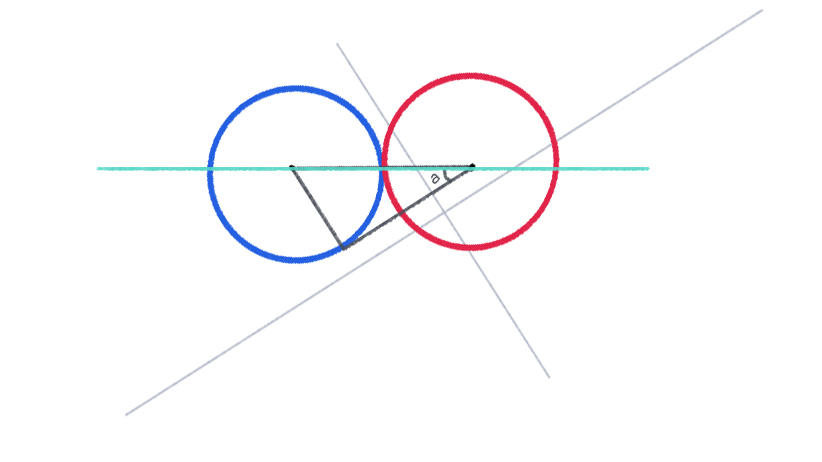
Lúc này ta có thể dễ dàng tính được vận tốc của 2 vật thể trước va chạm, sau đó tính được các bước tiếp theo theo công thức đã phân tích, như vậy mới có thể giải quyết được bài toán. Cuối cùng, chúng ta xoay đúng hệ toạ độ về góc ban đầu để chuyển động không trở nên “dị dạng” bởi góc lệch.

Kết bài

Bài toán đã được giải quyết, không quá khó, cũng không phải đơn giản nhỉ. Nó khó khi chúng ta không thể phân tích được bài toán, và nó trở nên dễ dàng hơn khi chúng ta đã hiểu về việc phải làm gì để thực hiện nó.

Ngoài vấn đề này ra, chúng ta còn rất nhiều vấn đề của Tin học sẽ đụng tới Toán, ví dụ như bạn lập trình một con AI đơn giản cho game Tic-Tac-Toe, bạn cũng cần sử dụng tới toán học để kiểm tra tính thắng thua trong trò chơi này.

Bạn không nhất thiết phải giỏi toán để trở thành một lập trình viên giỏi, đó là điều hiển nhiên. Nhưng ai cũng giỏi, vậy thì ai là người vượt trội hơn sẽ là người có lợi thế. Thời đại 4.0 rồi, chẳng có giới hạn nào trong cái ngành công nghệ này cả. Để cạnh tranh với những lập trình viên khác, bạn bắt buộc phải vượt trội.

Giá trị của bạn nằm ở việc bạn có những gì.

Good luck!

Tham khảo:

Elastic Collisions Using Vectors instead of Trigonometry - http://www.vobarian.com/collisions/
ElasticCollisions - http://www.themcclungs.net/physics/download/H/Momentum/ElasticCollisions.pdf
What are elastic and inelastic collisions? - https://www.khanacademy.org/science/physics/linear-momentum/elastic-and-inelastic-collisions/a/what-are-elastic-and-inelastic-collisions
Elastic Collisions In One Dimension Physics Problems - Conservation of Momentum & Kinetic Energy - https://youtu.be/CFbo_nBdBco
Elastic collision formula derivation if one of balls velocity is 0 - http://www.batesville.k12.in.us/physics/apphynet/Dynamics/Collisions/elastic_deriv.htm
Lec 16: Elastic and Inelastic Collisions - 8.01 Classical Mechanics, Fall 1999 (Walter Lewin) - https://youtu.be/ogiY6xt_TRM

Một số bài viết / sách hay:

How to think like a programmer — lessons in problem solving - https://www.freecodecamp.org/news/how-to-think-like-a-programmer-lessons-in-problem-solving-d1d8bf1de7d2/
Introduction to Mathematical Statistics - https://www.onlinemathlearning.com/statistics.html
Problem Solving with Algorithms and Data Structures - https://runestone.academy/runestone/books/published/pythonds/index.html
Programming and Mathematical Thinking - http://webpages.math.luc.edu/~lauve/courses/215-fa2016/Stavely_python_ebook.pdf
Mathematics by MIT Open Course ware - https://ocw.mit.edu/courses/audio-video-courses/#mathematics

Create (tạo), Read (đọc), Update (cập nhật) và Delete (xóa) dữ liệu phần mềm thông qua truy vấn ↩
atan2 là góc tan lượng giác ngược, trả về giá trị radian từ $-\pi$ tới $\pi$ giữa trục toạ độ x và tia từ gốc toạ độ $(0, 0)$ tới điểm $(x, y)$ , ví dụ $atan( \pm0, -0 ) = \pm\pi$ ↩